A few transmission line equations #
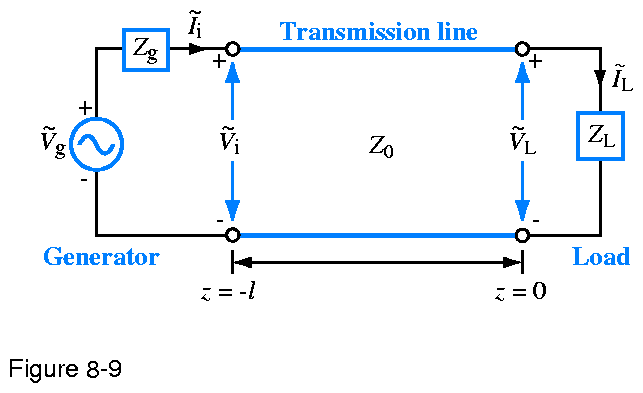
Figure 8.9: Transmission line of length \(l\) connected on one end to a generator circuit and on the other end to a load \(Z_{L}\). The load is located at \(z=0\) and the generator terminals are at \(z=l\).
source: https://eme2e.eecs.umich.edu/figs/f2.09.pdf (from https://eme2e.eecs.umich.edu/figs/figs8.html)
Equations #
Traveling wave solutions of the wave equations #
\[\gamma=\alpha+j\beta\]where \(\gamma\) is the complex propagation constant of the transmission line, \(\alpha\) is the attenutation constant of the line with units of \(\frac{\text{Np}}{\text{m}}\), \(\beta\) is the phase constant of the line with units of \(\frac{\text{rad}}{\text{m}}\).
In a lossless transmission line, \(\alpha=0\) and \(\gamma=j\beta\).
Spatial position \(z=-l\) corresponds to the sending end (generator terminals) and spatial position \(z=0\) corresponds to the location of the load. Coordinate \(d\) is defined as \(d=-z\) and denotes distance from the load.
\(\left(V_{0}^{+},I_{0}^{+}\right)\) are the wave amplitudes of the \(+z\) propagating wave and \(\left(V_{0}^{-},I_{0}^{-}\right)\) are the wave amplitudes of the \(-z\) propagating wave.
\[\Gamma=\frac{V_{0}^{-}}{V_{0}^{+}}=-\frac{I_{0}^{-}}{I_{0}^{+}}\]where \(\Gamma\) is the reflection coefficient.
The voltage phasor \(\tilde{V}\left(z\right)\) in a transmission line is
\[\begin{split} \tilde{V}\left(z\right)&=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z}\\ &=V_0^+\left(e^{-\gamma z}+\Gamma e^{\gamma z}\right)\\ &=V_0^+\left(e^{-\alpha z-j\beta z}+\Gamma e^{\alpha z+j\beta z}\right) \end{split}\] \[Z_{0}=\frac{V_{0}^{+}}{I_{0}^{+}}=-\frac{V_{0}^{-}}{I_{0}^{-}}\]where \(Z_{0}\) is the characteristic impedance of the line.
The current phasor \(\tilde{I}\left(z\right)\) in a transmission line is
\[\begin{split} \tilde{I}\left(z\right)&=I_{0}^{+}e^{-\gamma z}+I_{0}^{-}e^{\gamma z}\\ &=I_0^+\left(e^{-\gamma z}-\Gamma e^{\gamma z}\right)\\ &=I_0^+\left(e^{-\alpha z-j\beta z}-\Gamma e^{\alpha z+j\beta z}\right)\\ &=\frac{V_0^+}{Z_0}\left(e^{-\alpha z-j\beta z}-\Gamma e^{\alpha z+j\beta z}\right) \end{split}\]Magnitudes of the voltage and current phasors #
The magnitude of the voltage phasor \(\tilde{V}\left(z\right)\) in a transmission line is
\[ \begin{split} \left|\tilde{V}\left(z\right)\right|&=\left|V_0^+\right|\left(e^{-2\alpha z}+\left|\Gamma\right|^2e^{2\alpha z}+2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\left|V_0^+\right|\sqrt{e^{-2\alpha z}+\left|\Gamma\right|^2e^{2\alpha z}+2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)} \end{split} \]Note that some sources refer to \(\angle\Gamma\) as \(\theta_{\mathrm{r}}\), where \(\Gamma=\left|\Gamma\right|e^{j\angle\Gamma}=\left|\Gamma\right|e^{j\theta_{\mathrm{r}}}\).
The magnitude of the current phasor \(\tilde{I}\left(z\right)\) in a transmission line is
\[\begin{split} \left|\tilde{I}\left(z\right)\right|&=\frac{\left|V_0^+\right|}{\left|Z_0\right|}\left(e^{-2\alpha z}+\left|\Gamma\right|^2e^{2\alpha z}-2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\frac{\left|V_0^+\right|}{\left|Z_0\right|}\sqrt{e^{-2\alpha z}+\left|\Gamma\right|^2e^{2\alpha z}-2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)} \end{split}\]In a lossless transmission line (\(\alpha=0\)), these can be reduced to
\[\begin{split} \left|\tilde{V}\left(z\right)\right|&=\left|V_0^+\right|\left(1+\left|\Gamma\right|^2+2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\left|V_0^+\right|\sqrt{1+\left|\Gamma\right|^2+2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)} \end{split}\] \[\begin{split} \left|\tilde{I}\left(z\right)\right|&=\frac{\left|V_0^+\right|}{Z_0}\left(1+\left|\Gamma\right|^2-2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\frac{\left|V_0^+\right|}{Z_0}\sqrt{1+\left|\Gamma\right|^2-2\left|\Gamma\right|\cos\left(2\beta z+\angle\Gamma\right)} \end{split}\]Note that the characteristic impedance of a lossless transmission line is purely real, so \(\left|Z_{0}\right|=Z_{0}\) for a lossless line.
Since \(d=-z\) and cosine is an even function (\(\cos\left(-x\right)=\cos\left(x\right)\)), we also know that, for a lossless line,
\[ \begin{split} \left|\tilde{V}\left(d\right)\right|&=\left|V_0^+\right|\left(1+\left|\Gamma\right|^2+2\left|\Gamma\right|\cos\left(2\beta d-\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\left|V_0^+\right|\sqrt{1+\left|\Gamma\right|^2+2\left|\Gamma\right|\cos\left(2\beta d-\angle\Gamma\right)} \end{split} \] \[\begin{split} \left|\tilde{I}\left(d\right)\right|&=\frac{\left|V_0^+\right|}{Z_0}\left(1+\left|\Gamma\right|^2-2\left|\Gamma\right|\cos\left(2\beta d-\angle\Gamma\right)\right)^{\frac{1}{2}}\\ &=\frac{\left|V_0^+\right|}{Z_0}\sqrt{1+\left|\Gamma\right|^2-2\left|\Gamma\right|\cos\left(2\beta d-\angle\Gamma\right)} \end{split}\]Derivation of the magnitudes of the voltage and current phasors #
This can be derived using the formula for the voltage phasor in a lossless (\(\gamma=j\beta\)) transmission line \(\tilde{V}\left(z\right)=V_0^+\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)\). The derivation is as follows.
\[\left|\tilde{V}\left(z\right)\right|=\left(\tilde{V}\left(z\right)\tilde{V}^{*}\left(z\right)\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left(\left(V_0^+\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)\right)\left(\left(V_0^+\right)^{*}\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)^{*}\right)\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left(V_0^+\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)\left(V_0^+\right)^{*}\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)^{*}\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)\left(e^{-j\beta z}+\Gamma e^{j\beta z}\right)^{*}\right)^{\frac{1}{2}}\] \[\Gamma=\left|\Gamma\right|e^{j\theta_r}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j\beta z}\right)\left(e^{-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j\beta z}\right)^{*}\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j\beta z}\right)\left(\left(e^{-j\beta z}\right)^{*}+\left(\left|\Gamma\right|e^{j\theta_r}e^{j\beta z}\right)^{*}\right)\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j\beta z}\right)\left(e^{j\beta z}+\left|\Gamma\right|e^{-j\theta_r}e^{-j\beta z}\right)\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(1+\left|\Gamma\right|e^{-j\theta_r}e^{-j2\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j2\beta z}+\left|\Gamma\right|^2\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(1+\left|\Gamma\right|^2+\left|\Gamma\right|\left(e^{j\left(2\beta z+\theta_r\right)}+e^{-j\left(2\beta z+\theta_r\right)}\right)\right)^{\frac{1}{2}}\] \[e^{jx}+e^{-jx}=2\cos\left(x\right)\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(1+\left|\Gamma\right|^2+2\left|\Gamma\right|\cos\left(2\beta z+\theta_r\right)\right)^{\frac{1}{2}}\]Note that in the lossy case (\(\gamma=\alpha+j\beta\)), the result is
\[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-\alpha z-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{\alpha z+j\beta z}\right)\left(e^{-\alpha z-j\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{\alpha z+j\beta z}\right)^{*}\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(\left(e^{-\alpha z}e^{-j\beta z}+\left|\Gamma\right|e^{\alpha z}e^{j\theta_r}e^{j\beta z}\right)\left(e^{-\alpha z}e^{j\beta z}+\left|\Gamma\right|e^{\alpha z}e^{-j\theta_r}e^{-j\beta z}\right)\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(e^{-2\alpha z}+\left|\Gamma\right|e^{-j\theta_r}e^{-j2\beta z}+\left|\Gamma\right|e^{j\theta_r}e^{j2\beta z}+\left|\Gamma\right|^2e^{2\alpha z}\right)^{\frac{1}{2}}\] \[\left|\tilde{V}\left(z\right)\right|=\left|V_0^+\right|\left(e^{-2\alpha z}+\left|\Gamma\right|^2e^{2\alpha z}+2\left|\Gamma\right|\cos\left(2\beta z+\theta_r\right)\right)^{\frac{1}{2}}\]References #
See page 67 (Section 2-6.2: Standing Waves) of the following text:
Fawwaz Tayssir Ulaby and Umberto Ravaioli. Fundamentals of Applied Electromagnetics. Pearson. 8th edition, 2020. ISBN-10 0136681581. ISBN-13 9780136681588.
See page 261 (PDF page 276) (Section 8-5.2: Standing Waves) of the following text: https://www.fulcrum.org/ebooks/0p0969731/download (ISBNs: 9781607859116 (hardcover); 9781607859123 (open access, electronic))
The above link is from https://doi.org/10.3998/mpub.13073174 https://www.fulcrum.org/concern/monographs/r781wk11q
https://athena.ecs.csus.edu/~milica/EEE161/lecturenotes/TransmissionLines.pdf